HEIGHTS & DISTANCES

 

HEIGHTS & DISTANCES

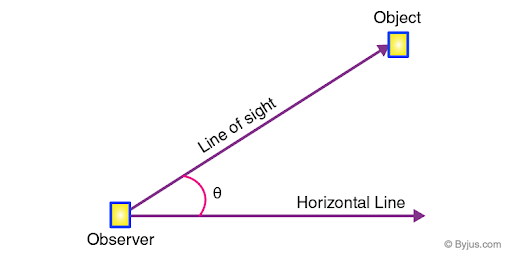
Definition: Angles of Elevation and Depression

Angle of Elevation :  An angle of elevation denotes the angle created by the line of sight of an observer and a horizontal line for an object above the horizontal.

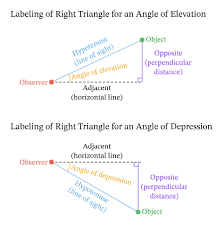
Angle of Depression : An angle of depression denotes the angle created by the line of sight of an observer and a horizontal line for an object below the horizontal.

1. The angle of elevation of the top of a building of height 20√3 ft from a point on the ground is 60°. The distance of the point from the building is

a) 20ft

b) 30ft

c) 20Ѵ3ft

d) None

2. A man on the top of a tower, standing on the seashore finds that a boat coming towards him takes 10min. for the angle of depression to change from 30° to 60°. Find the time taken by the boat to reach the shore from this position.

a) 4min.

b) 5min.

c) 6min.

d) 10min.

3. A man is standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a light house as 60° and the angle of depression of the base of lighthouse as 30°. Find the height of the light house.

a) 30m

b) 40m

c) 45m

d) 38m

4. Two ships are sailing in the sea on two sides of a lighthouse. The angles of elevation of the top of the lighthouse as observed from the two ships are 30° and 45° respectively. If the lighthouse is 100m high, the distance between the two ships is

a) 100m

b) 100Ѵ3m

c) 100(Ѵ3+1)m

d) None

 

5. A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank is 45°. When he moves 20m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree.

a) 10(√3 + 1)m

b) 15√3m

c) 200(√3 + 1)m

d) 10(√3 - 1)m

6.  From the top of a building 60m high, the angle of elevation and depression of the top and the foot of another building are α and β respectively. Find the height of the second building.

a) 60(1+ tan α tanβ)

b) 60(1+ cot α tanβ)

c) 60(1+ tan α cotβ)

d) 60(1- tan αcotβ)

7. A vertical post 15ft high is broken at a height and its upper part, not completely separated, meets the ground at angle of 30° . Find the height at which the post is broken.

a) 10ft

b) 5ft

c) 15√3 (2 - √3)ft

d) 5√3ft

8. The shadow of the tower becomes 60m longer when the altitude of the sun changes from 45°  to 30° . Then the height of tower is

a) 20 (√3 + 1) m

b) 24 (√3 + 1) m

c) 30 (√3 + 1) m

d) 30 (√3 − 1) m

9. When the angle of elevation of the sun increases from 30°  to 60° , the shadow of a post is diminished by 5m. Then, the height of the post is

a) 5√3/2 m

b) 2√3/5 m

c) 2/5√3 m

d) 4/5√3 m

 

10. From the top of a tower 75m high, the angles of depression of the top and bottom of a pole standing on the same plane as the tower are observed to be 30° and 45° respectively. Find the height of the pole.

a) 30.4m

b) 35.9m

c) 28.6m

d) 31.7m

11. A 10 m long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 60° and 45° respectively. Find the height of the tower.

a) 5(√3 + 1)m

b) 5(√3 + 3)m

c) 10(√3 - 1)m

d) 10(√3 + 1)m

12. The angles of elevation of the top of a tower from two points on the same side of the tower are α and β (α >β). If the distance between the two points is 40m, find the height of the tower.

a) 40cotαcotβ/(tanα + tanβ)

b) 40cotαtanβ/(tanα - tanβ)

c) 40tanαtanβ/(tanα - tanβ)

d) 40tanαtanβ/(tanα + tanβ)

13. The angle of elevation of the top of a tower from point A on the ground is 30°. On moving a distance of 40m towards the foot of the tower, the angle of elevation increases to 45°. Find the height of the tower.

a) 48.6m

b) 42.84m

c) 54.64m

d) 58.76m

14. An aeroplane, when 4000m high from the ground, pass vertically above another aeroplane at an instance when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 30° respectively. Find the vertical distance between the two aero planes.

a) 8000/3m

b) 8000/7m

c) 6000/7m

d) 1200m

15. A car is moving at uniform speed towards a tower. It takes 15 minutes for the angle of depression from the top of tower to the car to change from 30° to 60°. What time after this, the car will reach the base of the tower?

a) 6 min

b) 6.5 min

c) 7 min

d) 7.5 min

16. A man is watching from the top of a tower, a boat speeding away from the tower. The angle of depression from the top of the tower to the boat is 60° when the boat is 80m from the tower. After 10 seconds, the angle of depression becomes 30°. What is the speed of the boat? (Assume that the boat is running in still water).

a) 20 m/sec

b) 10 m/sec

c) 16 m/sec

d) 18 m/sec

17. There are two temples, one each bank of a river, just opposite to each other. One temple is 54m high. From the top of this temple, the angles of depression of the top & foot of the other temple are 30° & 60° respectively. Find the the width of the river & the height of the other temple.

18. From a point 'P' on the ground the angle of elevation of the top of a 10m tall building is 30°. A flag is hoisted at the top of the building  & the angle of elevation  of the top of the flagstaff from 'P' is 45°. Find the length of the flag staff? (Ans. 10(√3 −1)m)

19. From a point on a level of ground the angle of elevation to the top of the tower is 60°. If the tower is 346m high, what is the distance of the point from the foot of the tower? (√3 = 1.73)

a) 346√3m

b) 173m

c) 100m

d) 200m

20.  Two poles of equal heights are standing opposite to each other on either side of a road which is 100m wide. From a point between them on road, angles of elevation of their tops are 30° and 60°. The height of each pole in metre is 

a) 25√3 m

b) 20√3 m

c) 28√3 m

d) 30√3 m

 

N.B: Do all the problems and match with the given answers. If you have any doubt, please put in the comment box, I will definitely solve with explain details.